martes, 14 de abril de 2015
Ángulos de elevación y de depresión
Que es?

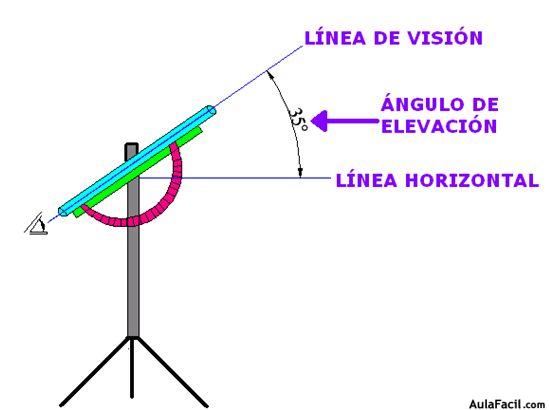
Ángulo de elevación
Es el ángulo vertical (agudo) formado por la línea horizontal y la
Es el ángulo vertical (agudo) formado por la línea horizontal y la
línea visual cuando el objeto o punto observado se encuentra
arriba de la línea horizontal.
Ángulo de depresión
Es el ángulo vertical (agudo) formado por la línea horizontal y la
línea visual cuan el objeto o punto observado está debajo de la
línea horizontal.


problemas de de aplicación de las razones trigonométricas y de ángulos de depresión y elevación
Problemas

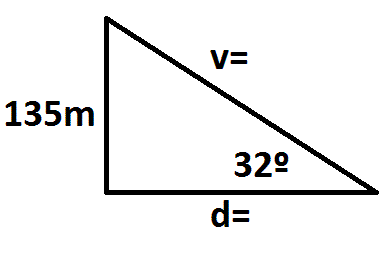
Hallamos d con la función tangente, ya que conocemos el cateto opuesto al ángulo de 32º y vamos a buscar el cateto adyacente

Ahora calculamos la visual v (hipotenusa) con la función Seno de 32º

Ambos resultados, al trabajarlos directamente en la calculadora científica, ofrecen un poco de diferencia en los decimales.
Ejemplo 2.
Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste.
Solución. Nótese cómo se elabora la gráfica cuando se trata de ángulo de depresión, el cual aparece fuera del triángulo que que se genera, pero es igual al otro ángulo alterno interno
La información se muestra en la gráfica.
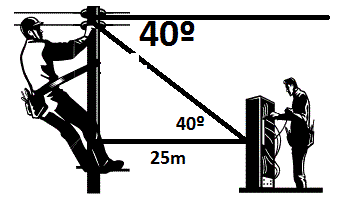
Observemos que el ángulo de depresión se trasladó al interior del triangulo
NOTA: Vemos así que el ángulo de elevación, siempre es igual al ángulo de depresión, y la visual es la hipotenusa.
Calculamos con tangente de 40º la altura h del poste.
Recuerden que uno de los indicadores de desempeño es: Formular, resolver y argumentar problemas .
Favor mostrar en su, cuaderno, el proceso para llegar a la respuesta correspondiente en cada ejercicio.
1. El piloto de un avión observa a un hombre en la calle de una ciudad con un ángulo de depresión de 42°, como se muestra en la figura:

Pregunta 1: Si la visual del piloto es de 15.95 km, la altura del avión en ese momento es:
A. 9.52 km
B. 8.77 km
C. 11.85m
D. 11.85 km
Pregunta 2: La horizontal del piloto (distancia entre el avión y la ciudad) mide aproximadamente:
A. 12.85 km
B. 10.67 km
C. 19.67 km
D. 11.93 km
Ejercicio 2. Un navegante ubica (fondea) su barco a 50 m del pie de un faro y observa la torre de éste con un ángulo de elevación de 53°, (ver figura)

PROBLEMA 3
Dos personas A y B separadas por "a" metros observan el campanario de una iglesia, como lo muestra la figura de abajo. A observa con un ángulo de elevación del 60º y B lo observa con un ángulo de elevación de 45º. ¿Cuál es la altura del campanario?
Un piloto de un barco observa al vigía de un faro con un ángulo de elevación de 32º. Si la altura del faro es de 135 m, calcular la distancia del faro al barco, y la visual del piloto.
(Una observación muy válida: si fuera el vigilante del faro el que observara al piloto del barco, entonces hablaríamos de angulo de depresión)
Solución.
Observemos la figura.
Se ha generado un triangulo rectángulo, recto en la base del faro. La visual del piloto es la hipotenusa, el ángulo de elevación está formado con la hipotenusa y la horizontal, Luego podemos construir un triangulo auxiliar donde ubicaremos a información suministrada, o si lo prefiere en el mismo dibujo.

Hallamos d con la función tangente, ya que conocemos el cateto opuesto al ángulo de 32º y vamos a buscar el cateto adyacente

Ahora calculamos la visual v (hipotenusa) con la función Seno de 32º

Ambos resultados, al trabajarlos directamente en la calculadora científica, ofrecen un poco de diferencia en los decimales.
Ejemplo 2.
Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste.
Solución. Nótese cómo se elabora la gráfica cuando se trata de ángulo de depresión, el cual aparece fuera del triángulo que que se genera, pero es igual al otro ángulo alterno interno
La información se muestra en la gráfica.

Observemos que el ángulo de depresión se trasladó al interior del triangulo
NOTA: Vemos así que el ángulo de elevación, siempre es igual al ángulo de depresión, y la visual es la hipotenusa.
Calculamos con tangente de 40º la altura h del poste.
Usted está en capacidad de hallar la medida de la visual (v), es decir, de la hipotenusa. Por favor use la función Coseno de 50º (La respuesta es 32,76 m)
EJERCICIOSRecuerden que uno de los indicadores de desempeño es: Formular, resolver y argumentar problemas .
Favor mostrar en su, cuaderno, el proceso para llegar a la respuesta correspondiente en cada ejercicio.
1. El piloto de un avión observa a un hombre en la calle de una ciudad con un ángulo de depresión de 42°, como se muestra en la figura:

Pregunta 1: Si la visual del piloto es de 15.95 km, la altura del avión en ese momento es:
A. 9.52 km
B. 8.77 km
C. 11.85m
D. 11.85 km
Pregunta 2: La horizontal del piloto (distancia entre el avión y la ciudad) mide aproximadamente:
A. 12.85 km
B. 10.67 km
C. 19.67 km
D. 11.93 km
Ejercicio 2. Un navegante ubica (fondea) su barco a 50 m del pie de un faro y observa la torre de éste con un ángulo de elevación de 53°, (ver figura)

Concepto de las funciones trigonométricas
¿Que es?



Concepto de función trigonométrica
Una función trigonométrica, también llamada circular, es aquella que se define por la aplicación de una razón trigonométrica a los distintos valores de la variable independiente, que ha de estar expresada en radianes. Existen seis clases de funciones trigonométricas: seno y su inversa, la cosecante; coseno y su inversa, la secante; y tangente y su inversa, la cotangente. Para cada una de ellas pueden también definirse funciones circulares inversas: arco seno, arco coseno, etcétera.
La función seno
Se denomina función seno, y se denota por f (x) 5 sen x, a la aplicación de la razón trigonométrica seno a una variable independiente x expresada en radianes. La función seno es periódica, acotada y continua, y su dominio de definición es el conjunto de todos los números reales.

Gráfica de la función seno.
La función cosecante puede calcularse como la inversa de la función seno expresada en radianes.
La función coseno
La función coseno, que se denota por f (x) = cos x, es la que resulta de aplicar la razón trigonométrica coseno a una variable independiente x expresada en radianes. Esta función es periódica, acotada y continua, y existe para todo el conjunto de los números reales.

Gráfica de la función coseno.
La función secante se determina como la inversa de la función coseno para un ángulo dado expresado en radianes.
La función tangente
Se define función tangente de una variable numérica real a la que resulta de aplicar la razón trigonométrica tangente a los distintos valores de dicha variable. Esta función se expresa genéricamente como f (x) = tg x, siendo x la variable independiente expresada en radianes.

Gráfica de la función tangente.
La función cotangente es la inversa de la tangente, para cualquier ángulo indicado en radianes.
describe y muestra la representación gráfica de las funciones trigonométricas

Representación gráfica de una función periódica
En la vida diaria existen muchos casos de funciones periódicas cuando la variable es el tiempo; situaciones como el movimiento de las manecillas de un reloj o las fases de la luna muestran un comportamiento periódico. Un movimiento periódico es aquel en el que la posición(es) del sistema se pueden expresar en base a funciones periódicas, todas con el mismo período.
Para una función aplicada al conjunto de los números reales o al de los enteros, significa que la totalidad de su gráfica puede ser representada a partir de copias de una determinada porción de ésta, repetida a intervalos regulares.
Las funciones trigonométricas seno, coseno típicos de funciones periódicas, cuyo período es 360 grados. En el caso de la tangente, vemos que su periodo es menor, siendo 180 grados.
problemas de aplicación de las funciones trigonométricas
problemas
1) Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?
Solucion:
1) Un dirigible que está volando a 800 m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se halla?
Solucion:
2) Calcular el área de una parcela triangular, sabiendo que dos de sus lados miden 80 m y 130 m, y forman entre ellos un ángulo de 70°.
Solucion:
3)Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa bajo un ángulo de 30° y si nos acercamos 10 m, bajo un ángulo de 60°.
Solución:
4)Tres pueblos A, B y C están unidos por carreteras. La distancia de A a C es 6 km y la de B a C 9 km. El ángulo que forman estas carreteras es 120°. ¿Cuánto distan A y B?
Solución:
Identidades trigonométricas
como determinar las identidades trigonométricas
Identidades trigonométricas fundamentales
1Relación seno coseno
cos² α + sen² α = 1
2Relación secante tangente
sec² α = 1 + tg² α
3Relación cosecante cotangente
cosec² α = 1 + cotg² α



Razones trigonométricas en un triángulo rectángulo
Seno
El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa.

Se denota por sen B.

Coseno
El coseno del ángulo B es la razón entre el cateto contiguo al ángulo y la hipotenusa.
Se denota por cos B.

Tangente
La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo.
Se denota por tg B.

Cosecante
La cosecante del ángulo B es la razón inversa del seno de B.
Se denota por cosec B.

Secante
La secante del ángulo B es la razón inversa del coseno de B.
Se denota por sec B.

Cotangente
La cotangente del ángulo B es la razón inversa de la tangente de B.
Se denota por cotg B.

Suscribirse a:
Entradas (Atom)



















Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triangulo rectángulo asociado a sus ángulos.
Existen seis funciones trigonométricas básicas.
Para definir las razones trigonométricas del ángulo: α, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:
- La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
- El cateto opuesto (a) es el lado opuesto al ángulo que queremos determinar.
- El cateto adyacente (b) es el lado adyacente al ángulo del que queremos determinar.
Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para angulos de este rangoEl valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo α , en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:
3) La tangente de un es la relación entre la longitud del cateto opuesto y la del adyacente:
4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:
5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:
6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto: